
题目:输入一个整型数组,数组里有正数也有负数。数组中一个或连续的多个整数组成一个子数组。
求所有子数组的和的最大值。要求时间复杂度为O(n)
例如输入的数组为{1,-2,3,10,-4,7,2,-5}
看到该题目,很多人都能想到最直观的方法,即枚举出数组的所有子数组并求出他们的和。一个长度为n的数组,总共有n(n+1)/2个子数组。计算出所有的子数组的和,最快也需要O(n2)的时间。通常最直观的方法不会是最优的方法,面试官将提示我们还有更快的方法。
解法一:举例分析数组的规律:
我们试着从头尾逐个累加示例数组中的每个数字。初始化和为0.第一步 加上第一个数字,此时和为1.接下来第二步加上数字-2,和就编程了-1.第三步加上数字3.我们注意到由于此前累计的和为-1,小于0,那如果用-1加 3,得到的和为2,比3本身还小。也就是说从第一个数字开始的子数组的和会小于从第三个数字开始的子数组的和。因此我们不用考虑从第一个子数组,之前累计 的和也被抛弃。
我们从第三个数字重新开始累加,此时得到的和为3.接下来第四步加 10,得到和为13.第五步加上-4,和为9.我们发现-4是一个负数,因此累加-4之后得到的和比原来的还小。因此我们要把之前得到的和13保存下来, 它有可能是最大的子数组的和。第六步加上数字7,9加7的结果是16,此时和比之前最大的和13还要大,把最大的子数组的和由13更新为16.第七步加上 2,累加得到的和为18,同时我们也要更新最大子数组的和。第八步加上最后一个数字-5,由于得到结果为13,小于此前得到的最大和18,因此最终最大的 子数组的和为18,对应的子数组是{3,10,-4,7,2}。
把过程分析清楚之后,我们用Java代码实现:
package cglib;
public class jiekou {
public int findGreatestSubArray(int[] array){
if(array==null||array.length<0) return 0; int currentSum=0; int greatestSum=0; for(int i=0;i<array.length;i++) { System.out.println("array[i]:"+array[i]); System.out.println("currentSum:"+currentSum); if(currentSum<=0){ System.out.println("currentSum<=0"); currentSum=array[i]; System.out.println("赋值后:currentSum:"+currentSum); }else{ System.out.println("currentSum>0"); currentSum+=array[i]; System.out.println("相加后:currentSum:"+currentSum); } if(currentSum>greatestSum){ System.out.println("currentSum>greatestSum"); System.out.println("currentSum:"+currentSum); System.out.println("greatestSum:"+greatestSum); greatestSum=currentSum; System.out.println("赋值后greatestSum:"+greatestSum); } } System.out.println("返回greatestSum:"+greatestSum); return greatestSum; } /** * args */ public static void main(String[] args) { jiekou p=new jiekou(); int[] array={1,-2,3,10,-4,7,2,-5}; System.out.println(p.findGreatestSubArray(array)); } } 输出:array[i]:1
currentSum:0 currentSum<=0 赋值后:currentSum:1 currentSum>greatestSum currentSum:1 greatestSum:0 赋值后greatestSum:1 array[i]:-2 currentSum:1 currentSum>0 相加后:currentSum:-1 array[i]:3 currentSum:-1 currentSum<=0 赋值后:currentSum:3 currentSum>greatestSum currentSum:3 greatestSum:1 赋值后greatestSum:3 array[i]:10 currentSum:3 currentSum>0 相加后:currentSum:13 currentSum>greatestSum currentSum:13 greatestSum:3 赋值后greatestSum:13 array[i]:-4 currentSum:13 currentSum>0 相加后:currentSum:9 array[i]:7 currentSum:9 currentSum>0 相加后:currentSum:16 currentSum>greatestSum currentSum:16 greatestSum:13 赋值后greatestSum:16 array[i]:2 currentSum:16 currentSum>0 相加后:currentSum:18 currentSum>greatestSum currentSum:18 greatestSum:16 赋值后greatestSum:18 array[i]:-5 currentSum:18 currentSum>0 相加后:currentSum:13 返回greatestSum:18 18解法二:应用动态规划法
我们还可以适用动态规划的思想来分析这个问题。如果用函数f(i)表示以第i个数字结尾的子数组的最大和,那么我们需要求出max[f(i)],其中0<=i<n。我们可以使用能够下面的递归公示求f(i):
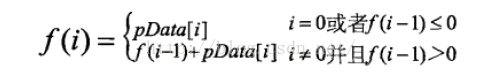
这个公式的意义:当以第i-1个数字结尾的子数组中所有的数字的和小 于0时,如果把这个负数与第i个数累加,得到的结果比第i个数字本身还要小,所以这种情况下以第i个数字结尾的子数组就是第i个数字本身。如果以第i-1 个数字结尾的子数组中所有的数字的和大于0,与第i个数字累加就得到以第i个数字结尾的子数组中所有的数字的和。
虽然我们用递归的方法分析动态规划的问题,但最终都会基于循环去编码。
- 使用动态规划方法来实现:
- *如果用函数f(i)表示以第i个数字结尾的子数组的最大和,那么我们需要求出max(f[0...n])。
- *我们可以给出如下递归公式求f(i)
- * |-- array[i] 如果i==0或者f(i-1)<0
- *f(i)=|
- * |-- f(i-1) + array[i] 如果f(i-1)>0
- *这个公式的意义:
- * 当以第(i-1)个数字为结尾的子数组中所有数字的和f(i-1)小于0时,如果把这个负数和第i个数相加,得到的结果反而比第i个数本身还要小,所以这种情况下最大子数组和是第i个数本身。
- * 如果以第(i-1)个数字为结尾的子数组中所有数字的和f(i-1)大于0,与第i个数累加就得到了以第i个数结尾的子数组中所有数字的和。
package cglib;
public class jiekou {
public int findGreatestSubArray(int[] array){
if(array==null||array.length<0) return 0; int[] c=new int[array.length];//用来记录以当前元素结尾(数组就到当前元素的位置为止)的子数组的最大和 int max = -1000;//用来记录数组c[]中的最大值 int start = 0;//记录数组中子数组的最大和的开始位置 int end = 0;//记录数组中子数组的最大和的结束位置 int tmp = 0; c[0] = array[0]; System.out.println("c[0]:"+c[0]); for(int i = 1;i < array.length;++i) { System.out.println("array[i]:"+array[i]); System.out.println("c[i-1]:"+c[i-1]); if(c[i-1] > 0) { System.out.println("c[i-1]大于0"); c[i] = c[i-1] + array[i]; System.out.println("c[i]:"+c[i]); } else { System.out.println("c[i-1]小于0"); c[i] = array[i]; System.out.println("c[i]:"+c[i]); tmp = i; System.out.println("tmp:"+tmp); } if(c[i] > max) { System.out.println("c[i]大于max"); max = c[i]; start = tmp; end = i; } } System.out.println("子数组最大和的起始位置:"+start+"~"+end); System.out.println("最大值max:"+max); return max; } /** * args */ public static void main(String[] args) { jiekou p=new jiekou(); int[] array={1,-2,3,10,-4,7,2,-5}; System.out.println(p.findGreatestSubArray(array)); } } 输出:c[0]:1
array[i]:-2 c[i-1]:1 c[i-1]大于0 c[i]:-1 c[i]大于max array[i]:3 c[i-1]:-1 c[i-1]小于0 c[i]:3 tmp:2 c[i]大于max array[i]:10 c[i-1]:3 c[i-1]大于0 c[i]:13 c[i]大于max array[i]:-4 c[i-1]:13 c[i-1]大于0 c[i]:9 array[i]:7 c[i-1]:9 c[i-1]大于0 c[i]:16 c[i]大于max array[i]:2 c[i-1]:16 c[i-1]大于0 c[i]:18 c[i]大于max array[i]:-5 c[i-1]:18 c[i-1]大于0 c[i]:13 子数组最大和的起始位置:2~6 最大值max:18 18